Esoteric Update #268 - We Embedded Springs
Alright, so the strings were indeed embedded.
I've spent the last week implementing this tool, and I think it was worth it because the results were exactly what I hoped for. Let's go over what I did and how it ended up working.
First, I started with a simple algorithm, Eades' Spring algorithm. I intended to get something going so I could judge progress on everything. If this gave bad results, I could move to something more intricate. But apart from some minor issues with the whole graph ballooning, it looked close to what I wanted to achieve. I decided to keep the method but work on it a bit. I implemented forces from the Fruchterman-Reingold method with a C = 1 (this means that the desired distance between nodes is 1 unit of length; later on, I made this value differ for edges connected to the root so that the clustering around the root relaxes a little bit), and this already vastly improved the results. I also implemented my own idea by weighting the forces based on the degree of the node; this is something I noticed in passing in Tutte's Barycentric algorithm. I've not implemented anything specifically from it; I just took some inspiration on what can be done. Finally, I also added edge repulsion, an idea that exists for graph drawing in general, but again, I didn't base it on any specific method.
Now, edge repulsion leads to some problems, as it promotes modes getting "caught" against random edges. When everything goes well, it leads to better results, and the caught nodes can be dealt with manually.
Secondly, I implemented a series of terminal commands that control the whole process. This is a dual-window application. One window is the terminal, and the other is the display, which visualises the graph. From the terminal, you can call various commands to modify the graph.
Here's just a random graph constructed using the application:
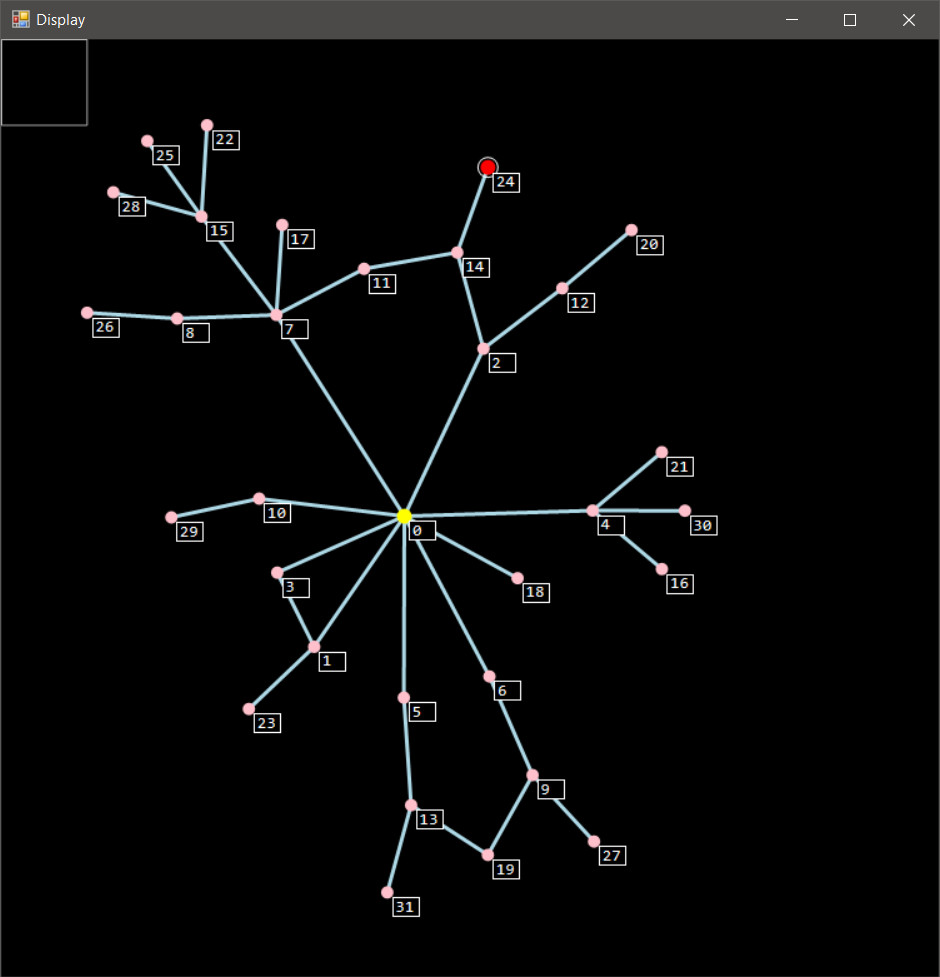
The grey outline in the upper left corner is a unit square for reference. Based on it, we can see that, as stated before, the distance between nodes tends towards 1 unit unless something gets in the way.
Now for some crucial tests: how will it deal with a circle and when all other nodes connect to the root:
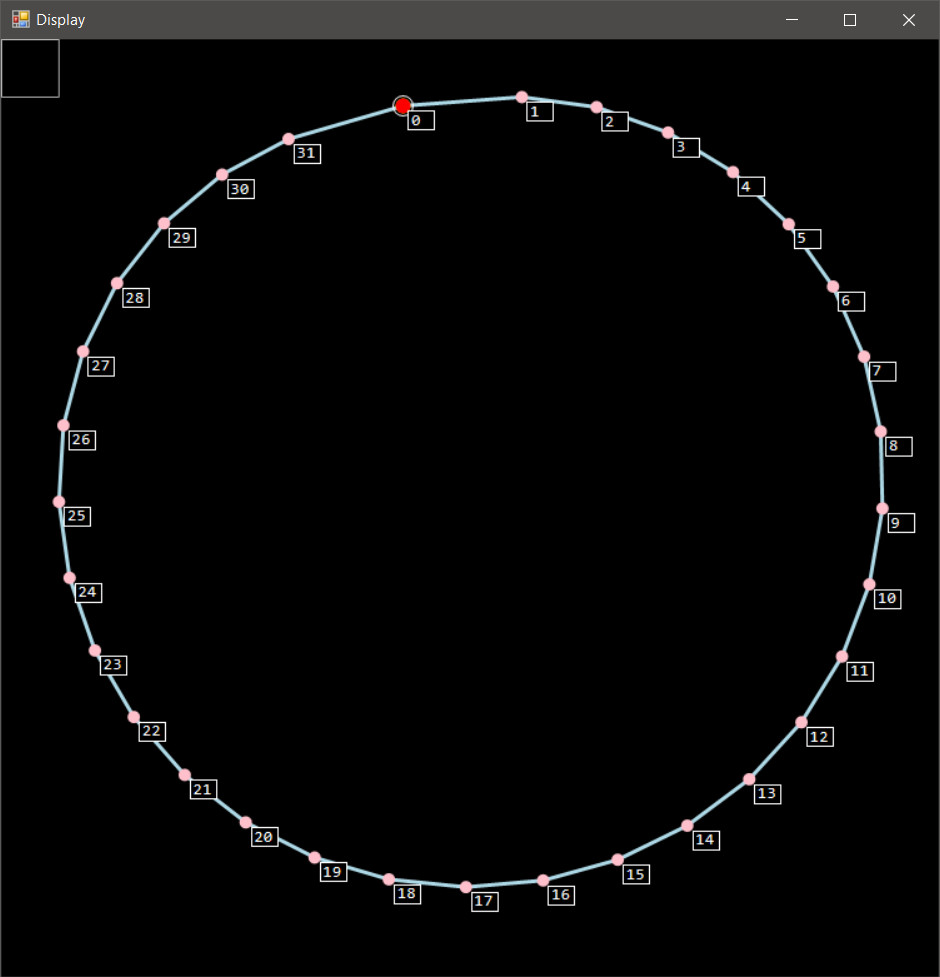
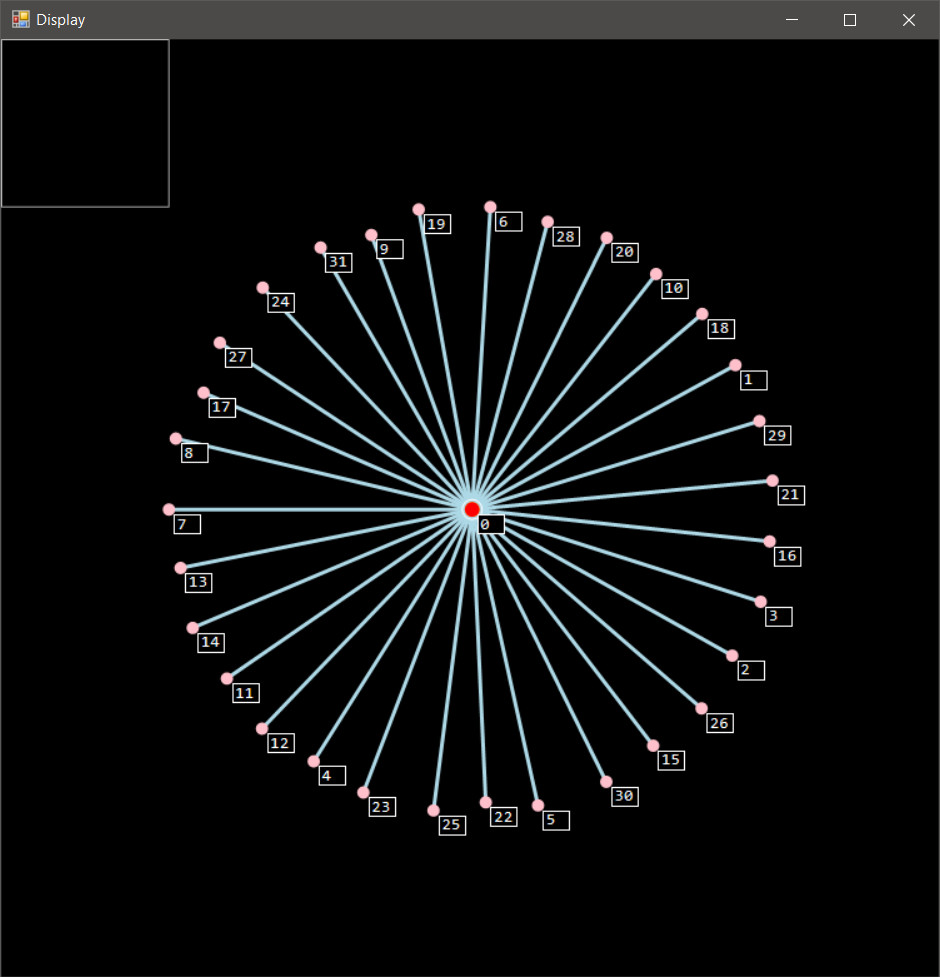
These are the desired results, showing that the graph is laid out correctly for some cases where we know what the exact result should be.
Now for a more process-driven demonstration. Let's see how we take a random graph from beginning to end, and I'll also show the commands used to achieve the final positioning of nodes.
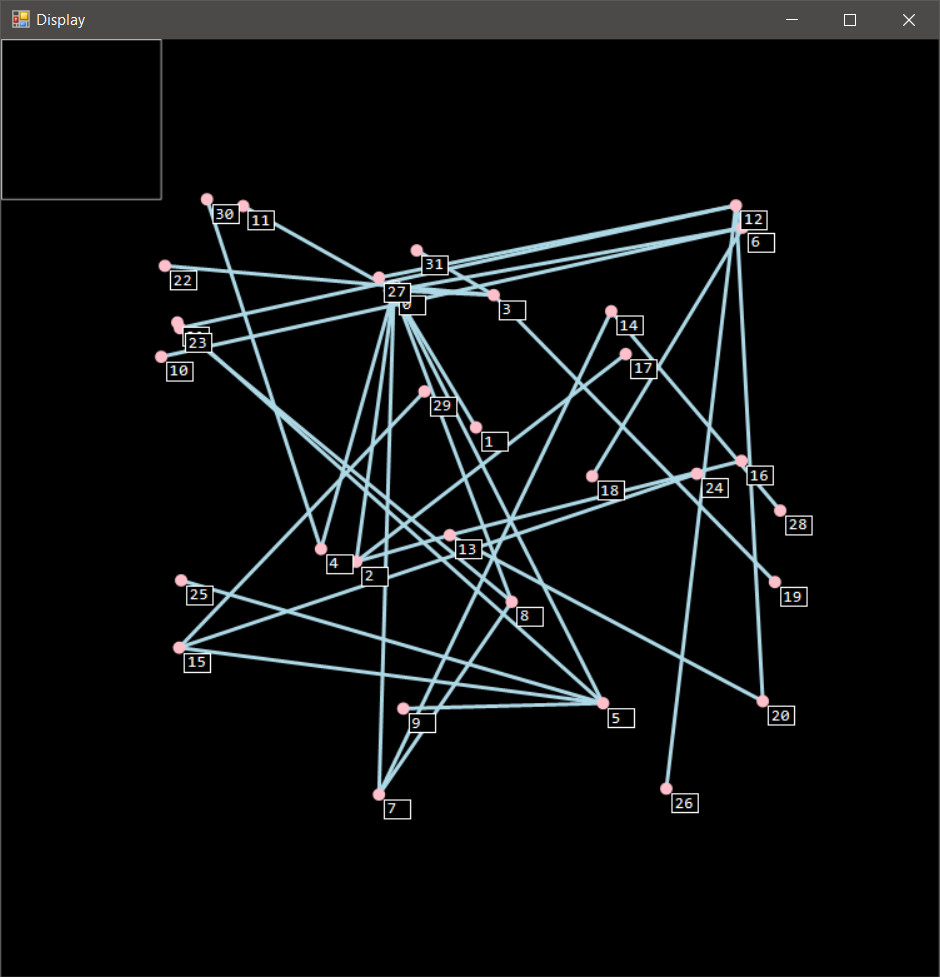
We start with a random positioning of the nodes.
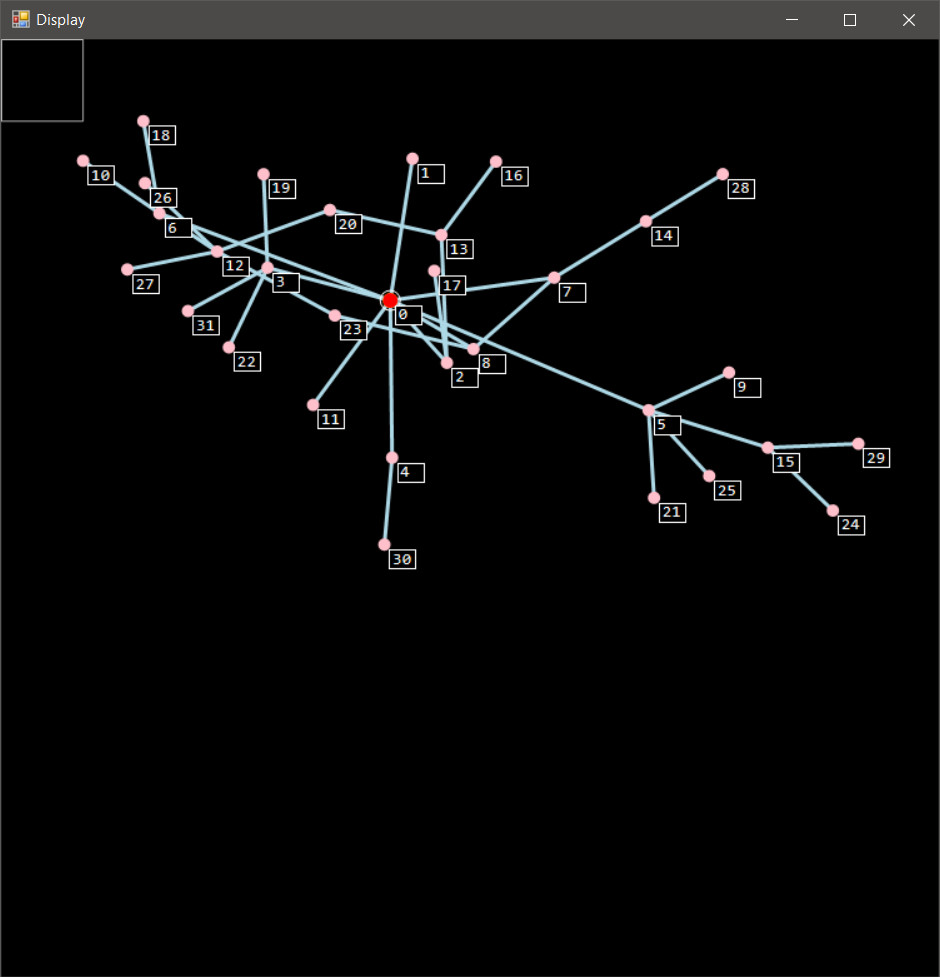
Then, we let the algorithm work. Some nodes got tangled up, but that's the point of being able to edit the results. It may not be evident to you, but some simple corrections need to be made, and then there will be a non-trivial issue involving some loops. We'll start by resolving the simple problems.
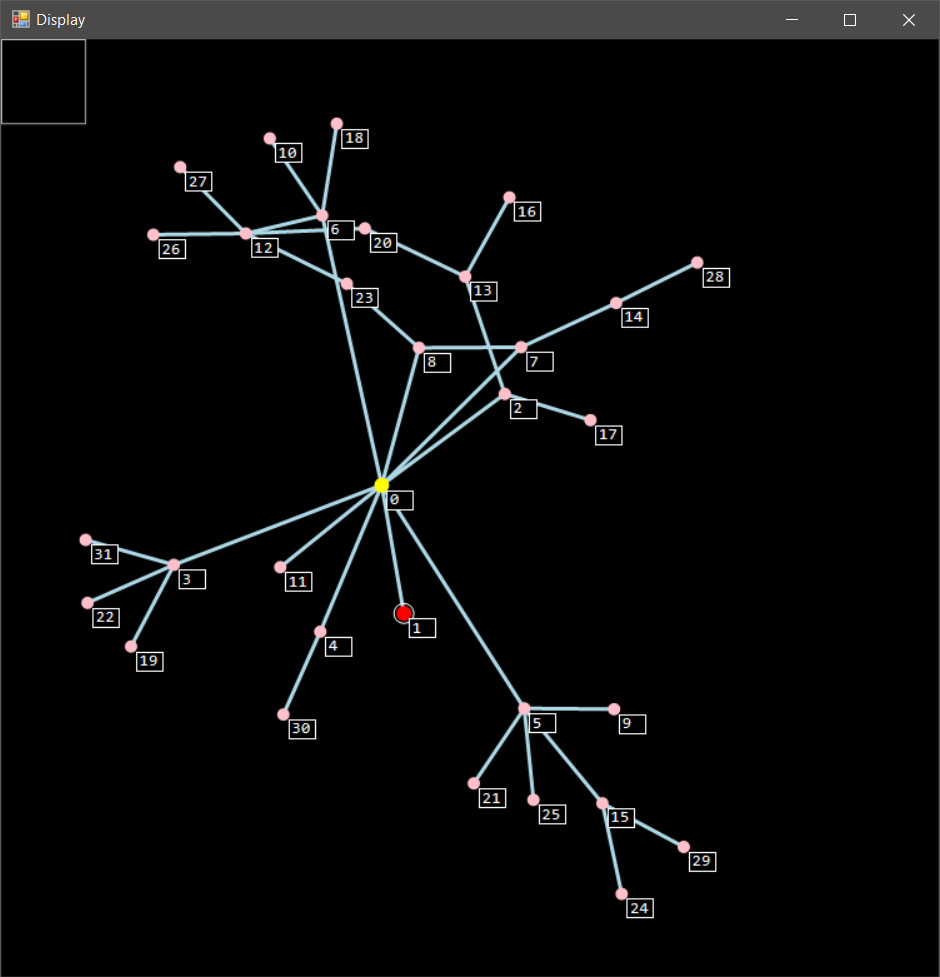
This leaves us with the loops.
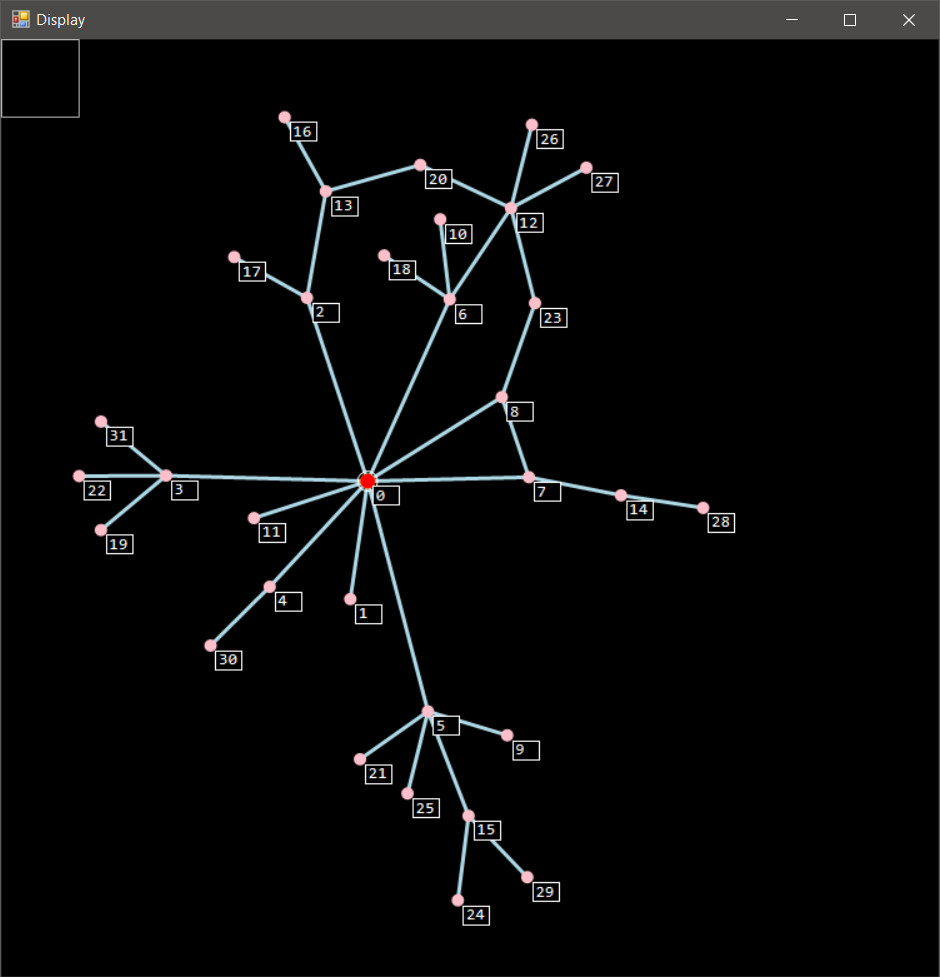
In the end, we have the final position of the nodes after untangling the loops.
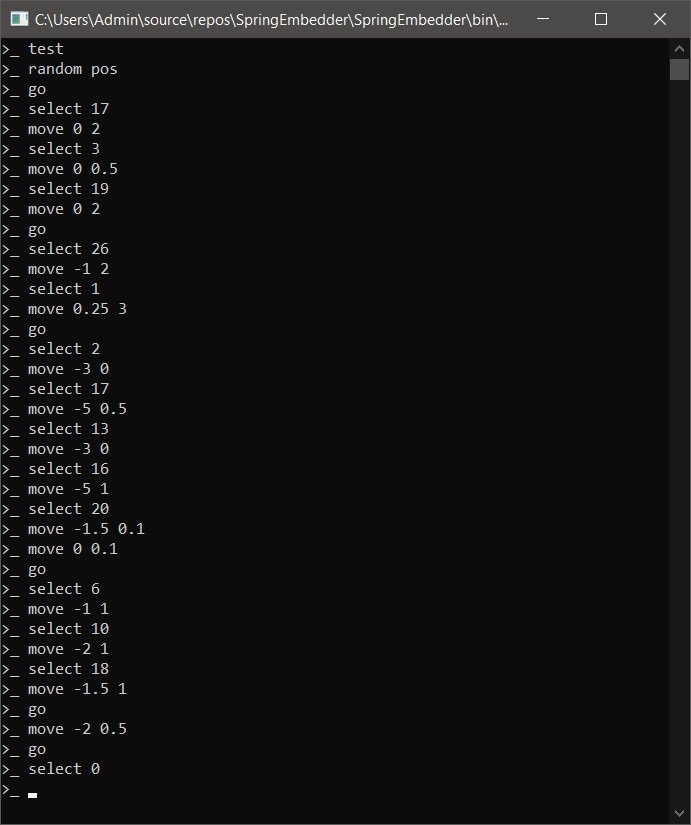
The sequence of commands isn't particularly long, even though this test presents a more problematic graph arrangement.
So, this has been a success; it does exactly what I want it to do. The only thing I need to add is the ability to import and export data. I also want to try one more idea related to "exclusive" nodes, that is, nodes that will never appear on the mind map together but are part of the same map.
Get Esoteric ♥ Esoterica
Esoteric ♥ Esoterica
A story driven erotic game about magic, supernatural forces, love and BDSM.
| Status | In development |
| Author | EsoDev |
| Genre | Interactive Fiction |
| Tags | Erotic, Experimental, Fantasy, Female Protagonist, Mystery, Procedural Generation, Romance, Story Rich, Text based |
| Languages | English |
| Accessibility | Color-blind friendly, High-contrast |
More posts
- Grieving, Updates Paused10 days ago
- Esoteric Update #336 - Unfortunately English Grammar Exists14 days ago
- Esoteric Update #335 - Archetypes of Appearance22 days ago
- Esoteric Update #334 - Phrases Revisited28 days ago
- Esoteric Update #333 - Happy Independence Day35 days ago
- Esoteric Update #332 - Tooltip Triumphs42 days ago
- Esoteric Update #331 - Tooltip Troubles49 days ago
- Esoteric Update #330 - Reactive Character Creation57 days ago
- Esoteric Update #329 - And Out of the Hospital63 days ago
- Esoteric Update #328 - An Update From The Hospital70 days ago
Leave a comment
Log in with itch.io to leave a comment.